Statistical Tolerance Intervals in MedTech – Explained Based on ISO 16269-6

A statistical tolerance interval is an estimated interval calculated from sample data that can be stated, with a given confidence level (e.g., 95%), to contain at least a specified proportion p of the population.

In other words, if we randomly sample from a production process, we can calculate an interval that, with 95% confidence, covers at least p% of all future units. The endpoints of this interval are often called the statistical tolerance limits (lower and upper).

According to ISO 16269-6 (Statistical interpretation of data – Part 6: Determination of statistical tolerance intervals), the interval is constructed such that it includes at least the fraction p of the population with a specified confidence level [3].

Both one-sided and two-sided statistical tolerance intervals are defined: a one-sided interval has only one limit (either lower or upper); in contrast, a two-sided interval has both an upper and a lower limit.

To visualize this, consider a normal distribution curve (the classic “bell curve”).

This curve is characterized by two parameters: the mean (μ) and the standard deviation (σ).

For a normally distributed characteristic, such as a physical dimension measured on every product in a batch, most values cluster around the mean μ, with variability described by σ.

You might recall that approximately 68.3% of the values in a normal distribution fall within ±1σ of the mean. This is illustrated by the green shaded area in the figure below, which corresponds to one standard deviation on either side of the mean.

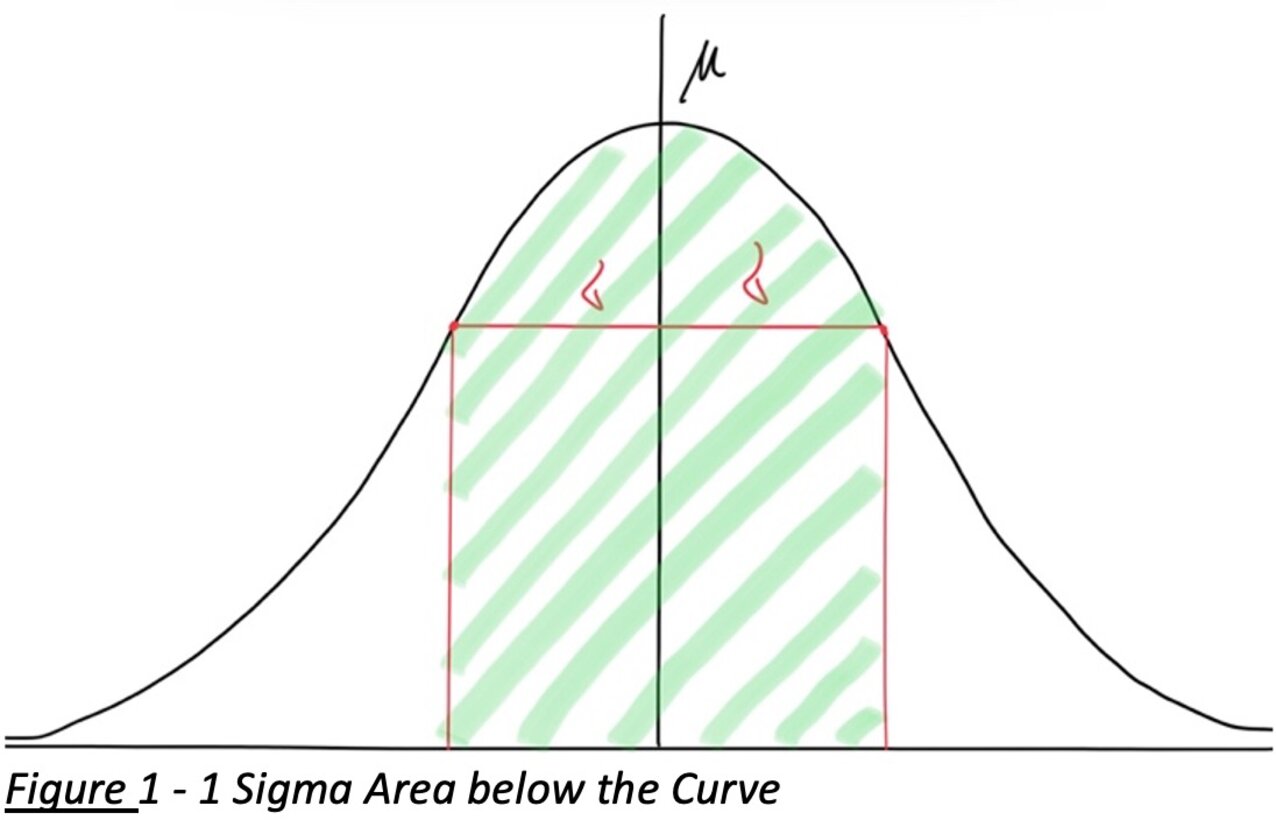
Figure 1: A normal distribution curve showing the mean (μ) and standard deviation (σ). About 68.3% of the population lies within ±1σ of the mean (green shaded region), assuming a normal sample. This property is the basis for many statistical methods in quality control and forms the foundation for statistical tolerance intervals.

Knowing μ and σ for a given continuous distribution allows us to predict what proportion of products will fall within any given range.

However, statistical tolerance intervals go beyond simply using the known properties of the normal curve; they account for the uncertainty in estimating μ and σ from a sample. If we had an infinite population and knew its true μ and σ, we could say exactly what fraction lies between any two limits.

In reality, we only have a sample and thus uncertain estimates (sample mean and sample standard deviation). The tolerance interval introduces a confidence level to ensure that, despite this uncertainty, the interval will contain the desired proportion of the population.

It’s important to distinguish tolerance intervals from other statistical intervals:

• A confidence interval estimates a population parameter (like the true mean) with a given confidence level. It answers a question about a parameter’s likely range, not about individual data points. For example, a 95% confidence interval for the mean tells us where the true mean may lie, but not how the data are spread.

• A prediction interval predicts the range for a single future observation (or a small number of future observations) with a given confidence. It’s about one future sample at a time.

• A tolerance interval, in contrast, is constructed to contain a specified proportion of the population (e.g., 95% of all items) with a given confidence (e.g., 95%). It addresses the spread of actual data points. In essence, while a prediction interval covers a specified proportion on average, a tolerance interval guarantees (with confidence) that at least that proportion of the entire population (or any future repeated random samples from it) is covered.

Because tolerance intervals focus on population coverage, they are highly relevant for conformity assessment in manufacturing. They answer questions like: “With 95% confidence, does at least 99% of my product meet the specification limits?”

This is crucial in quality control applications for medical devices, where patient safety is on the line. If the tolerance interval falls within the product’s specification limits, we can claim with high confidence that the vast majority of units will be within spec, which is often a regulatory expectation.

In the medical device industry, everything revolves around risk management and patient safety. Our entire industry is risk-based; even the Quality Management System standard (ISO 13485:2016) explicitly calls for risk-based approaches (see ISO 13485:2016, 4.1.2b).

We assess the probability of occurrence for each potential failure or harm. Many of these probabilities pertain to manufacturing variability. For instance, a sequence of events could lead to harm (like a device malfunction causing injury), and some of those events originate in production (e.g., a dimension out of tolerance leading to device failure). We need to know how frequently such problems might occur in production.

Statistical tolerance intervals provide a straightforward way to quantify the likelihood that product measurements remain within safe limits. By knowing the process mean μ and standard deviation σ for a critical characteristic, and computing a tolerance interval, we can estimate the proportion of products that are nonconforming (OOS - out of spec) with a given confidence. This is literally a lifesaver – if we can say with 95% confidence that 99% of products meet all requirements, we significantly reduce the risk to patients.

Another reason tolerance intervals are useful in MedTech is that regulators and standards often expect a high degree of confidence (most of the time at least 95%) in process performance. Tolerance intervals inherently combine confidence level and population proportion into one statement. For instance, a “95/90 tolerance interval” (95% confidence, 90% proportion) is a common criterion. Some Notified Bodies in the EU even ask for 95% confidence with 95% proportion (or higher) for critical parameters, reflecting a very stringent expectation of quality.

From a Regulatory Affairs perspective, using statistical tolerance intervals demonstrates a data-driven, scientifically justified approach to showing compliance with specifications. It aligns with regulatory guidance to use appropriate statistical techniques for design verification and process validation.

From a Quality Engineering perspective, tolerance intervals help in determining sample sizes and acceptance criteria for validation. Instead of arbitrary sampling, one can use ISO 16269-6 tables or formulas to decide how many units to test to be confident in the results. In fact, ISO 16269-6 can be used to derive statistical sampling plans in process validation that are focused on consumer risk (the patient’s risk) rather than producer’s risk .

In traditional acceptance sampling, an Acceptable Quality Limit (AQL) is often used, which focuses on producer’s risk of rejecting a good batch. However, for validation in MedTech, we care more about patient’s risk – ensuring with high confidence that a bad batch would be detected. Thus, we use a Rejectable Quality Level (RQL) approach. AQL-based plans are not optimal for patient safety unless the corresponding consumer risk is justified, whereas RQL-based plans and statistical tolerance intervals directly address the consumer’s risk of nonconformance.

From a Production perspective, establishing a statistical tolerance interval for a process characteristic means that production can be monitored and controlled to stay within that interval. It provides a clear, quantitative goal for process capability. If the process drifts, routine sampling might show the tolerance interval encroaching on specification limits, signaling it’s time for process adjustment or maintenance. In this way, tolerance intervals integrate into statistical process management and continuous improvement: they translate variability into the language of risk and conformance.

The concept of statistical tolerance intervals assumes normal distribution of the data. However, assuming normality is not enough – we must verify it.

In practice, that means performing a normality test on the sample data. If the data pass the normality test, we can justify using the parametric formula for tolerance intervals that assumes a normal sample. If the data fail the normality test (meaning we have to reject the null hypothesis H₀ that the data come from a normal distribution), then using the normal-based approach may be invalid.

There are many ways to test for normality (e.g. Shapiro-Wilk, Anderson-Darling tests, etc., often available in statistical software like Minitab, R, JMP, SPSS, MATLAB, etc. ). Typically, we choose a significance level (α, often 0.05 or 0.01). If the test yields a p-value below α, we conclude the data are not normally distributed (reject H₀).

Common reasons for failing a normality test include [1]:

• The underlying distribution is truly not normal (different shape).

• The dataset contains outliers or is a mixture of two distributions (e.g. data from two machines mixed together).

• The measurement resolution is too low (a coarse measurement can mask distribution shape).

• The data are skewed (asymmetry).

• Large sample size – with very large n, even tiny deviations from normality can cause a test to fail (practically, normality tests are most reliable for sample sizes roughly 15 to 100 points [2]).

Failing a normality test is not necessarily a disaster. It just means the assumption for the straightforward approach is violated. We have several options to address this [2]:

• Investigate outliers: If an outlier is due to a measurement error or an assignable cause, you might justify removing or correcting it.

• Use Higher Capability Acceptance Criteria: If the process capability (e.g., Ppk) is very high, even non-normal data can be acceptable because it’s far within specs. A very high capability means the fraction nonconforming is so low that normality matters less. In fact, if Ppk is above a certain threshold, one can statistically show the product is conforming with high confidence without assuming normality .

• Use a Skewness-Kurtosis specific normality test: Certain normality tests (like D’Agostino-Pearson) consider skewness and kurtosis. If the data fail a generic test but still have acceptable skewness and kurtosis relative to spec limits, they might be considered “normal enough” for tolerance interval purposes.

• If the data meet acceptance criteria (e.g., all values well within specs) and other lots of the product are normally distributed, one might argue the non-normal sample is an anomaly or at least not concerning.

• Use an attribute sampling plan instead: If you truly cannot treat the data as normal, you might resort to a distribution-free (non-parametric) approach or even treat the outcome as pass/fail and use attribute methods (like ANSI/ISO 2859 sampling plans). This is less efficient (usually requires larger sample size) but makes no distribution assumption.

Let’s take a closer look at two common strategies when normality fails:

1) Higher Capability Acceptance Criteria

If your sample data show extremely high capability (say Ppk >> 1.33), the process is so tightly controlled that almost all data are well within specifications. Wayne Taylor [2] suggests that in such cases you can accept the process without assuming normality because the margin to the spec is large.

What is “sufficiently high” capability?

It depends on sample size and the chosen RQL (Rejectable Quality Level). Essentially, one can derive a required Ppk such that even a non-normal distribution would yield an acceptably low fraction out of spec.

For example, based on the sample size and RQL, a multiplier is applied to Ppk/Pp to set new acceptance criteria . If the process meets that elevated Ppk requirement, you pass validation without needing normality.

2) Skewness-Kurtosis Specific Normality Test

Some processes produce data that are consistently skewed (e.g., many measurements near one limit).

A standard normality test might fail, but a closer look shows the distribution isn’t pathological, just skewed. For instance, if you have a positively skewed distribution (tail to the right, as shown in the figure below), and only a lower specification limit applies, the skewness might not actually jeopardize product quality – most values are well above the lower limit.

Specialized normality tests can focus on whether the tails are longer than a normal distribution in a way that would increase risk of hitting a spec limit . If not, the data might be considered effectively normal for our purposes.

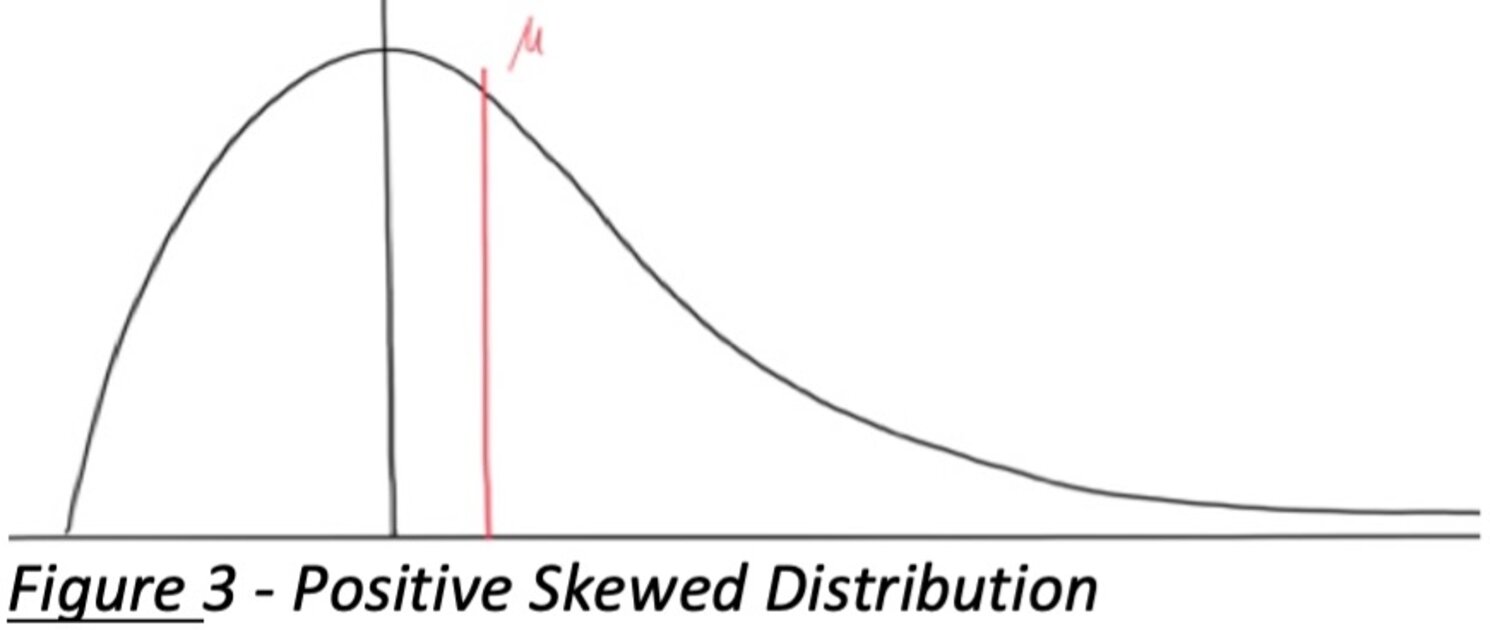
Figure 3: Positively skewed distribution (right tail). In this example, a lower spec limit (SL) is the only requirement. The mean (μ) is not at the peak of the curve (mode) due to skewness. For skewed distributions, mean, median, and mode differ (μ > mode for positive skew). If such data still meet acceptance criteria (e.g., the entire tolerance interval lies above the lower limit), a skewness-focused normality test might pass even if a general normality test fails. The normality assumption must be carefully evaluated whenever data are skewed.

In any case where the normality assumption cannot be validated, ISO 16269-6 provides a distribution-free (non-parametric) method as well. This method does not assume any specific distribution, requiring larger sample sizes but guaranteeing coverage for a continuous distribution. For example, if nothing is known about the distribution except that it’s continuous, one can use non-parametric tolerance intervals (basically based on order statistics) to be safe. This is akin to using an attribute method (pass/fail criteria) but framed as a tolerance interval. It’s less powerful than the parametric method for a given sample size, which is why proving normality (and using the parametric method) is preferred in most cases.

... where xL and xU are the lower and upper statistical tolerance limits respectively.

The factor k (often called the tolerance factor) is determined by the chosen confidence level (e.g., 95%), the proportion p of the population to cover (e.g., 95% or 99%), and the sample size n.

Essentially, k is an inflated z-value accounting for sample uncertainty: higher confidence or higher p yields a larger k, while a larger sample size yields a smaller k (more precision).

ISO 16269-6 provides tables of exact k factors for various scenarios (one-sided or two-sided intervals, different n, p, and confidence). There are also formulas or software to compute k when tables are not available. Once we have k, we calculate the lower tolerance limit xL and/or upper tolerance limit xU. Depending on the specification limits of the product, we may only need one side:

• If we have only a lower specification limit (LSL) (for example, a strength must be ≥ X), we use a one-sided lower tolerance interval: xL = μ – k σ, and we compare xL to the LSL.

• If we have only an upper specification limit (USL) (for example, a contaminant must be ≤ Y), we use a one-sided upper tolerance interval: xU = μ + k σ, and we compare xU to the USL.

• If there are two specification limits (both a minimum and maximum), we compute both xL and xU for a two-sided interval, and ensure the interval [xL, xU] lies within [LSL, USL].

The acceptance criteria in a validation or verification context typically are:

• For a lower spec limit only: pass if xL ≥ LSL. (Our interval’s lower bound is above the minimum requirement.)

• For an upper spec limit only: pass if xU ≤ USL. (Our interval’s upper bound is below the maximum allowed.)

• For two-sided specs: pass if xL ≥ LSL and xU ≤ USL. In other words, the entire tolerance interval must fall inside the specification limits.

Let’s consider an example to cement this. Imagine we are validating the seal strength of a sterile barrier system (like the peel strength of sterile packaging). This is a common test in MedTech, and suppose our regulatory or internal requirement is that seal strength must be at least 1.2 N/15mm. So, LSL = 1.2 N/15mm (there is no upper limit in this case, more strength is fine - which is technically not correct, one still needs to be able to open the pouch, hence usability testing is required).

We choose a 95% confidence level and 95% population proportion for our tolerance interval (often called a “95/95” tolerance interval). (Note: Some regulators or Notified Bodies might require 95%/99%, but we’ll use 95%/95% for this example.) We take a sample of n = 30 sealed packages and test their strength. We find:

• Sample mean m = 10.28 N/15mm

• Sample standard deviation s = 0.76 N/15mm

The data appear roughly normal (which is reasonable for strength data if the sealing process is in control). Using ISO 16269-6, table C.2 (for a one-sided interval at 95%/95% with n=30) gives us a k-value (exact k factor) of 2.2199. This k essentially tells us how many standard deviations below the mean we need to go to capture 95% of the population with 95% confidence.

Now we calculate the lower tolerance limit:

xL = 10.28 - 2.2199 * 0.76 = 8.59N/15mm.

So xL ≈ 8.59 N/15mm. This is the 95%/95% statistical tolerance lower limit.

We compare xL to the specification LSL = 1.2 N/15mm. Clearly, 8.59 ≥ 1.2, so the criterion xL ≥ LSL is met by a wide margin. The test passes.

We can now make the confidence statement:

“With 95% confidence, at least 95% of the population of seal strengths is ≥ 8.59 N/15mm.”

Since 8.59 N/15mm is far above the required 1.2 N/15mm, effectively we’re saying with high confidence, essentially 100% of products exceed the spec in this case.

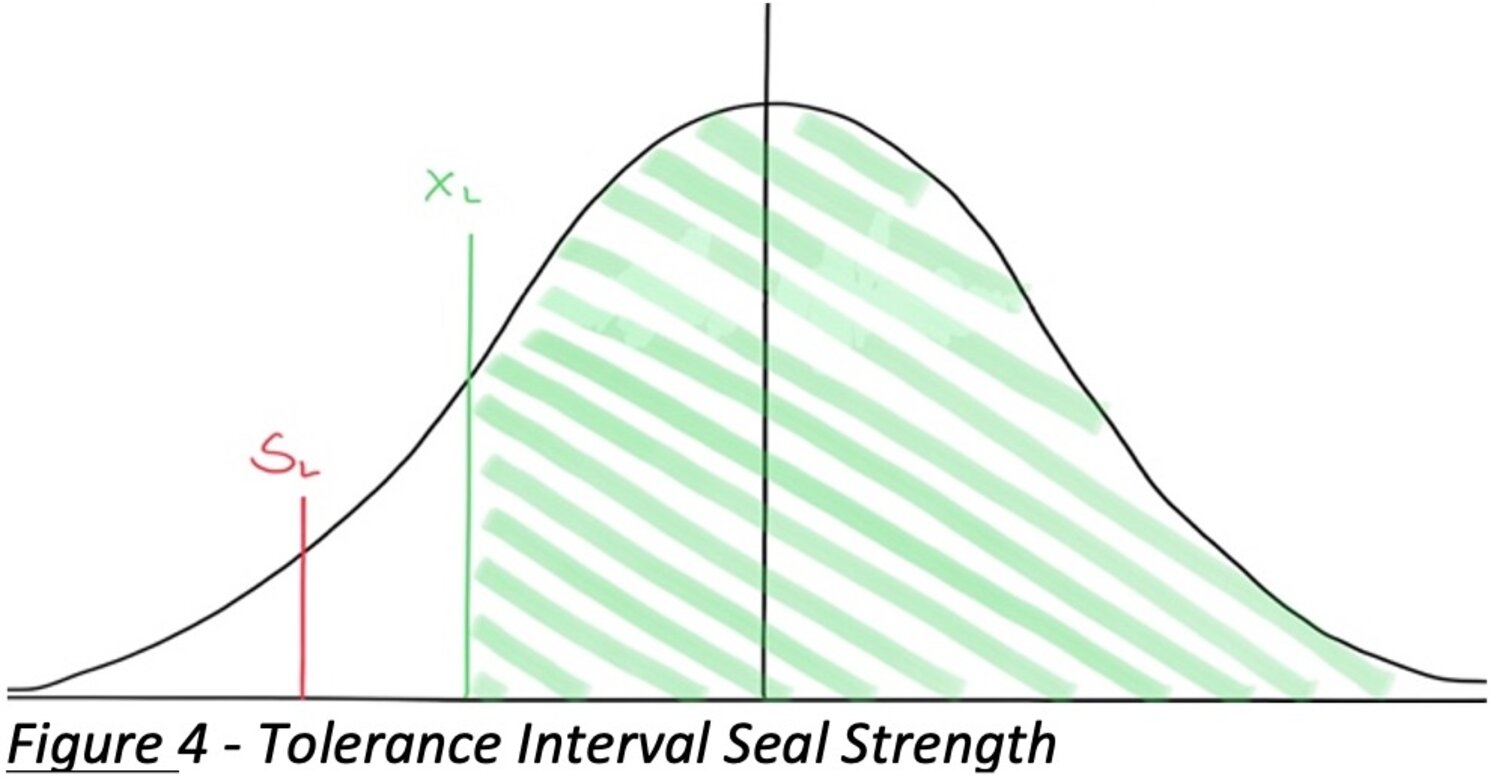
Figure 4: Statistical tolerance interval for the seal strength example. The curve represents the distribution of seal strengths (μ ≈ 10.28, σ ≈ 0.76). The green shaded area indicates the portion of the population (at least 95%) above the calculated lower tolerance limit xL ≈ 8.59 N.

The red line near the left represents the lower specification limit (LSL = 1.2 N). In this case, xL is much greater than LSL, so we have a large safety margin. We can conclude the process meets the requirement with room to spare, and the fraction of the population conforming is far above 95%.

A few observations from this example:

• If xL had been exactly equal to LSL, it would mean we are just barely meeting the “95% of population ≥ LSL” criterion. In other words, if xL = 1.2 N, we could only say “with 95% confidence, 95% of the population is ≥ 1.2 N”– that implies up to 5% of units could be below spec (the maximum allowed by the statistical tolerance interval statement). This would be a borderline accept, essentially the minimum to pass.

• In our case, xL is much higher than LSL. The greater the distance between xL and the spec limit, the higher the proportion of the population that is actually conforming – well above the required 95%. For instance, practically 100% of our seals are above 1.2 N because even the tolerance bound for 95% of them is 8.59 N, which is way above 1.2 N. This provides a huge confidence buffer.

• This illustrates why establishing statistical tolerance intervals makes sense: it quantifies the population conformity in a rigorous way. Rather than just saying “all 30 samples passed 1.2 N, so we’re good,” we are using that data to make an inference about all future units, with a defined confidence. It’s a much stronger statement for quality assurance and regulatory compliance.

In the example above, we dealt with a one-sided tolerance interval because there was only a lower spec limit. Many times in MedTech, requirements are one-sided (e.g., strength ≥ X, or impurity ≤ Y). In such cases, one-sided intervals are more powerful (they require smaller samples for the same confidence or yield tighter bounds) because you’re only covering one tail of the distribution.

If we had a requirement like a length must be between 90mm and 110mm (two-sided specs), that involves two limits. We would need a two-sided statistical tolerance interval – one that captures the middle p proportion of the population between an upper and lower bound. Two-sided intervals are wider than one-sided intervals for the same confidence and p, because covering p in both tails requires accounting for more variation.

ISO 16269-6 provides procedures for both types.

Two-sided intervals ensure that a proportion p of the population lies between xL and xU. For example, a 95%/99% two-sided interval would give bounds [xL, xU] such that 99% of the population is between those bounds, with 95% confidence. If that interval fits within the spec limits, it means at least 99% of products meet specs with 95% confidence.

It’s worth noting that ISO 16269-6 even covers combining data from multiple samples (e.g., multiple batches) when those samples are from normal distributions with a common but unknown variance. This is an advanced scenario where you pool data across batches to calculate a tolerance interval for the overall population. It requires statistical homogeneity of variance, but it’s useful if you want a single interval covering, say, all lots tested in a validation.

Establishing statistical tolerance intervals is a smart strategy for MedTech companies because it ties together statistical evidence and risk management in a structured, quantitative manner. Rather than guessing or over-testing, you use a method grounded in an international standard (ISO 16269-6) which is the result of consensus by ISO technical committees and adopted by various national standards bodies. This lends credibility to your verification/validation approach during audits or regulatory submissions.

Key benefits include:

• Patient Safety and Confidence: By using tolerance intervals, you directly address the question “what fraction of products could be out of spec?” with high confidence. This focuses on the fraction nonconforming (e.g., at most 5% if using 95%/95%) and ensures it’s acceptably low. It’s a more meaningful measure for patient safety than just sample averages or individual test results.

• Regulatory Compliance: This approach meets regulatory expectations for using statistical methods in product and process qualification. For example, FDA guidance and EU Notified Bodies recognize a 95%/99% tolerance interval approach as solid evidence that a process consistently produces conforming product, which is exactly what process validation aims to demonstrate.

• Efficiency in Sampling: Tolerance intervals help right-size your sampling plans. Instead of testing hundreds of units “just to be sure,” you can calculate exactly how many samples are needed to demonstrate a given confidence/proportion criterion. This ensures you meet the acceptable quality limit in terms of risk without unnecessary testing. Conversely, if your sample is too small, the tolerance interval will be wide, clearly showing that more data (or a different approach) is needed – preventing false confidence from inadequate sampling.

• Continuous Improvement: After initial validation, statistical tolerance intervals can be used in ongoing monitoring. They set a benchmark for process performance. If periodic re-sampling and analysis show that the tolerance interval is approaching or exceeding a spec limit, it’s an early warning that process variation may be increasing or the mean shifting. This allows proactive process adjustments or maintenance (thus tying into overall quality control applications and process control).

• Cross-Functional Communication: For Quality Engineers, tolerance intervals provide clear pass/fail criteria that incorporate statistical confidence. For Regulatory Affairs, they provide documented evidence and statements (e.g., “with X% confidence, at least Y% of products are within spec”) that can be included in submissions or technical files to satisfy regulatory concerns. For Production managers, the tolerance interval results translate into actionable metrics – for example, a requirement that the process mean be centered well away from the spec limits to ensure a high proportion conforming. In essence, tolerance intervals create a common language of quality that everyone understands.

In summary, statistical tolerance intervals (whether one-sided or two-sided) are a powerful tool in the statistical interpretation of data from manufacturing processes. They allow us to make statements about the true values of product characteristics in the population, based on sample data, in a scientifically rigorous way.

By establishing such intervals during design verification and process validation, a MedTech organization can ensure that the actual properties of their devices consistently meet requirements with a quantifiable level of confidence.

This not only helps in meeting regulatory and standards requirements, but – most importantly – provides confidence that patients and end-users receive devices that are safe and effective, backed by solid statistical evidence.